While filming herself getting ready for work recently, TikTok user @gracie.ham reached deep into the ancient foundations of mathematics and found an absolute gem of a question: "How could someone come up with a concept like algebra?"
She also asked what the ancient Greek philosopher Pythagoras might have used mathematics for, and other questions that revolve around the age-old conundrum of whether mathematics is "real" or something humans just made up.
Many responded negatively to the post, but others – including mathematicians like me – found the questions quite insightful.
Is mathematics real?
Philosophers and mathematicians have been arguing over this for centuries. Some believe mathematics is universal; others consider it only as real as anything else humans have invented.
Thanks to @gracie.ham, Twitter users have now vigorously joined the debate.
If she's asking how we uncover mathematical truths, are those truths real or constructed etc indicates she likely got an A in algebra without even trying
— Lauren Pleska 🏳️🌈 (@RadFemme74) August 28, 2020
can we blow this one up instead of the one where i sound stupid hashtag math isn't real pic.twitter.com/HuaEDwqXXP
— gracie cunningham | BLM (@graciegcunning) August 27, 2020
For me, part of the answer lies in history.
From one perspective, mathematics is a universal language used to describe the world around us. For instance, two apples plus three apples is always five apples, regardless of your point of view.
But mathematics is also a language used by humans, so it is not independent of culture. History shows us that different cultures had their own understanding of mathematics.
Unfortunately, most of this ancient understanding is now lost. In just about every ancient culture, a few scattered texts are all that remain of their scientific knowledge.
However, there is one ancient culture that left behind an absolute abundance of texts.
Babylonian algebra
Buried in the deserts of modern Iraq, clay tablets from ancient Babylon have survived intact for about 4,000 years.
These tablets are slowly being translated and what we have learned so far is that the Babylonians were practical people who were highly numerate and knew how to solve sophisticated problems with numbers.
Their arithmetic was different from ours, though. They didn't use zero or negative numbers. They even mapped out the motion of the planets without using calculus as we do.
Of particular importance for @gracie.ham's question about the origins of algebra is that they knew that the numbers 3, 4 and 5 correspond to the lengths of the sides and diagonal of a rectangle. They also knew these numbers satisfied the fundamental relation 3² + 4² = 5² that ensures the sides are perpendicular.
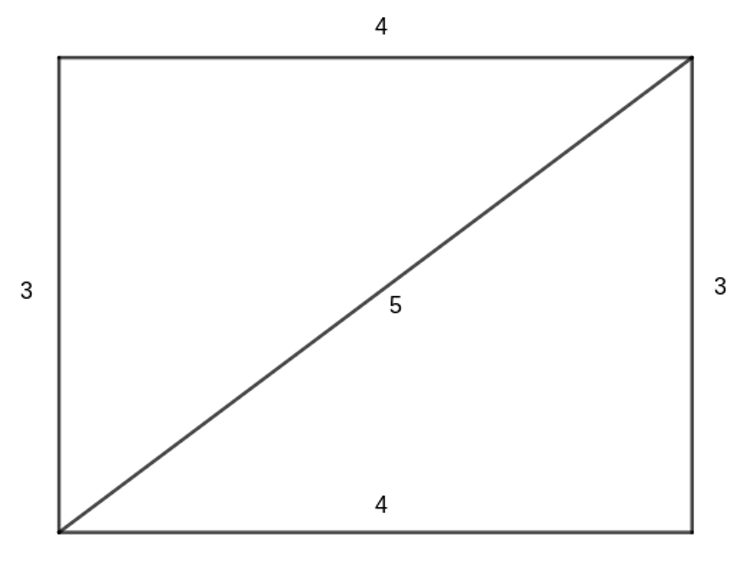
The Babylonians did all this without modern algebraic concepts. We would express a more general version of the same idea using Pythagoras' theorem: any right-angled triangle with sides of length a and b and hypotenuse c satisfies a² + b² = c².
The Babylonian perspective omits algebraic variables, theorems, axioms and proofs not because they were ignorant but because these ideas had not yet developed. In short, these social constructs began more than 1,000 years later, in ancient Greece.
The Babylonians happily and productively did mathematics and solved problems without any of these relatively modern notions.
What was it all for?
@gracie.ham also asks how Pythagoras came up with his theorem. The short answer is: he didn't.
Pythagoras of Samos (c. 570-495 BC) probably heard about the idea we now associate with his name while he was in Egypt. He may have been the person to introduce it to Greece, but we don't really know.
Pythagoras didn't use his theorem for anything practical. He was primarily interested in numerology and the mysticism of numbers, rather than the applications of mathematics.
The Babylonians, on the other hand, may well have used their knowledge of right triangles for more concrete purposes, although we don't really know. We do have evidence from ancient India and Rome showing the dimensions 3-4-5 were used as a simple but effective way to create right angles in the construction of religious altars and surveying.
Without modern tools, how do you make right angles just right? Ancient Hindu religious texts give instructions for making a rectangular fire altar using the 3-4-5 configuration with sides of length 3 and 4, and diagonal length 5. These measurements ensure that the altar has right angles in each corner.
Big questions
In the 19th century, the German mathematician Leopold Kronecker said "God made the integers, all else is the work of man".
I agree with that sentiment, at least for the positive integers – the whole numbers we count with – because the Babylonians didn't believe in zero or negative numbers.
Mathematics has been happening for a very, very long time. Long before ancient Greece and Pythagoras.
Is it real? Most cultures agree about some basics, like the positive integers and the 3-4-5 right triangle. Just about everything else in mathematics is determined by the society in which you live. ![]()
Daniel Mansfield, Lecturer in Mathematics, UNSW.
This article is republished from The Conversation under a Creative Commons license. Read the original article.
#Physics | https://sciencespies.com/physics/is-maths-real-thats-actually-a-much-smarter-question-than-you-might-think/
No comments:
Post a Comment